Covariance, Regression, and Correlation

Covariance

Variance measures the dispersion of a univariate distribution. The covariance provides a natural measure of the association between two variables.

The covariance of \(x\) and \(y\) is defined to be the average of this quantity \((x-\mu_x)(y - \mu_y)\) over all pairs of measures in the population

\[ \begin{aligned} \sigma(x, y) &=E\left[\left(x-\mu_{x}\right)\left(y-\mu_{y}\right)\right] \\ &=E\left(x y-\mu_{y} x-\mu_{x} y+\mu_{x} \mu_{y}\right) \\ &=E(x y)-\mu_{y} E(x)-\mu_{x} E(y)+\mu_{x} \mu_{y} \\ &=E(x y)-\mu_{x} \mu_{y} \end{aligned} \]

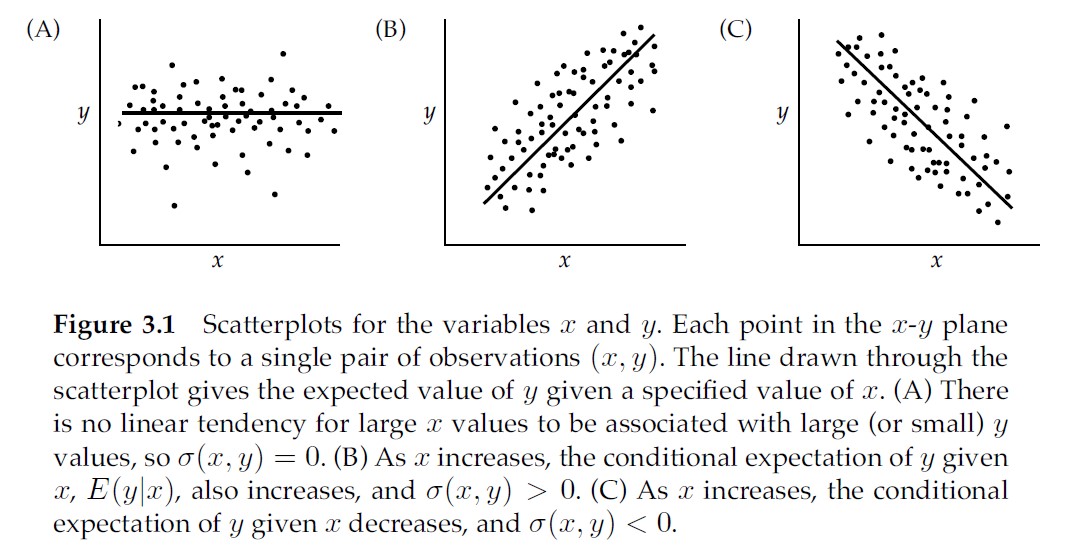
Regression

\[ y = \alpha + \beta x +e \]

\(\alpha\) is \(y\)-intercept, \(\beta\) is the slope, and \(e\) is the residual error.

\[ \hat{y} = \alpha +\beta x \]

\[ \begin{array}{c} e^{2}=(y-\bar{y})^{2}-2 b(y-\bar{y})(x-\bar{x})+b^{2}(x-\bar{x})^{2}+(a+b \bar{x}-\bar{y})^{2} \\ -2(y-\bar{y})(a+b \bar{x}-\bar{y})+2 b(x-\bar{x})(a+b \bar{x}-\bar{y}) \end{array} \]

\[ \overline{e^{2}}=\left(\frac{n-1}{n}\right)\left[\operatorname{Var}(y)-2 b \operatorname{Cov}(x, y)+b^{2} \operatorname{Var}(x)\right]+(a+b \bar{x}-\bar{y})^{2} \] \[ \begin{array}{l} \frac{\partial\left(\overline{e^{2}}\right)}{\partial a}=2(a+b \bar{x}-\bar{y})=0 \\ \frac{\partial\left(\overline{e^{2}}\right)}{\partial b}=2\left[\left(\frac{n-1}{n}\right)[-\operatorname{Cov}(x, y)+b \operatorname{Var}(x)]+\bar{x}(a+b \bar{x}-\bar{y})\right]=0 \end{array} \]

\[ \begin{array}{l} a=\bar{y}-b \bar{x} \\ b=\frac{\operatorname{Cov}(x, y)}{\operatorname{Var}(x)} \end{array} \]

\[ \begin{aligned} \operatorname{Cov}(x, e) &=\operatorname{Cov}[x,(y-a-b x)]=\operatorname{Cov}(x, y)-\operatorname{Cov}(x, a)-b \operatorname{Cov}(x, x) \\ &=\operatorname{Cov}(x, y)-0-b \operatorname{Var}(x) \\ &=\operatorname{Cov}(x, y)-\frac{\operatorname{Cov}(x, y)}{\operatorname{Var}(x)} \operatorname{Var}(x)=0 \end{aligned} \]

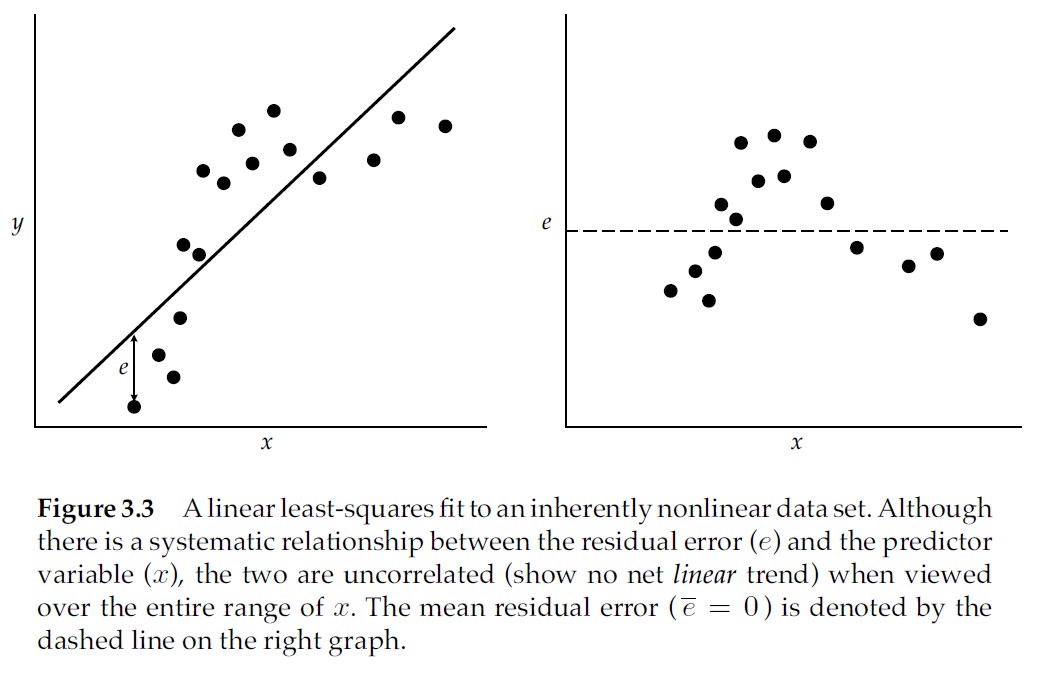
Correlation

For purposes of hypothesis testing, it is often desirable to use a dimensionless measure of association. The most frequently used measure in bivariate analysis is the correlation coefficient,

\[ r(x,y) = \frac{Cov(x, y)}{\sqrt{Var(x)Var(y)}} \]

\[ b(y, x) = r\sqrt{\frac{Var(y)}{Var(x)}} \]

\[ \begin{aligned} \operatorname{Var}(e) &=\operatorname{Var}(y-a-b x)=\operatorname{Var}(y-b x) \\ &=\operatorname{Var}(y)-2 b \operatorname{Cov}(x, y)+b^{2} \operatorname{Var}(x) \\ &=\operatorname{Var}(y)-\frac{2[\operatorname{Cov}(x, y)]^{2}}{\operatorname{Var}(x)}+\frac{[\operatorname{Cov}(x, y)]^{2} \operatorname{Var}(x)}{[\operatorname{Var}(x)]^{2}} \\ &=\left(1-\frac{[\operatorname{Cov}(x, y)]^{2}}{\operatorname{Var}(x) \operatorname{Var}(y)}\right) \operatorname{Var}(y)=\left(1-r^{2}\right) \operatorname{Var}(y) \end{aligned} \]

Therefore,

\[ r^2 = 1 - \frac{Var(e)}{Var(y)} \]