Nested Cross Validation
Original paper
Background
Cross-validation (CV) is an effective method for estimating the prediction error of a classifier. Some recent articles have proposed methods for optimizing classifiers by choosing classifier parameter values that minimize the CV error estimate. We have evaluated the validity of using the CV error estimate of the optimized classifier as an estimate of the true error expected on independent data.
Results
We used CV to optimize the classification parameters for two kinds of classifiers; Shrunken Centroids and Support Vector Machines (SVM). Random training datasets were created, with no difference in the distribution of the features between the two classes. Using these “null” datasets, we selected classifier parameter values that minimized the CV error estimate. 10-fold CV was used for Shrunken Centroids while Leave-One-Out-CV (LOOCV) was used for the SVM. Independent test data was created to estimate the true error. With “null” and “non null” (with differential expression between the classes) data, we also tested a nested CV procedure, where an inner CV loop is used to perform the tuning of the parameters while an outer CV is used to compute an estimate of the error.
The CV error estimate for the classifier with the optimal parameters was found to be a substantially biased estimate of the true error that the classifier would incur on independent data. Even though there is no real difference between the two classes for the “null” datasets, the CV error estimate for the Shrunken Centroid with the optimal parameters was less than 30% on 18.5% of simulated training data-sets. For SVM with optimal parameters the estimated error rate was less than 30% on 38% of “null” data-sets. Performance of the optimized classifiers on the independent test set was no better than chance.
The nested CV procedure reduces the bias considerably and gives an estimate of the error that is very close to that obtained on the independent testing set for both Shrunken Centroids and SVM classifiers for “null” and “non-null” data distributions.
Conclusion
We show that using CV to compute an error estimate for a classifier that has itself been tuned using CV gives a significantly biased estimate of the true error. Proper use of CV for estimating true error of a classifier developed using a well defined algorithm requires that all steps of the algorithm, including classifier parameter tuning, be repeated in each CV loop. A nested CV procedure provides an almost unbiased estimate of the true error.
One example
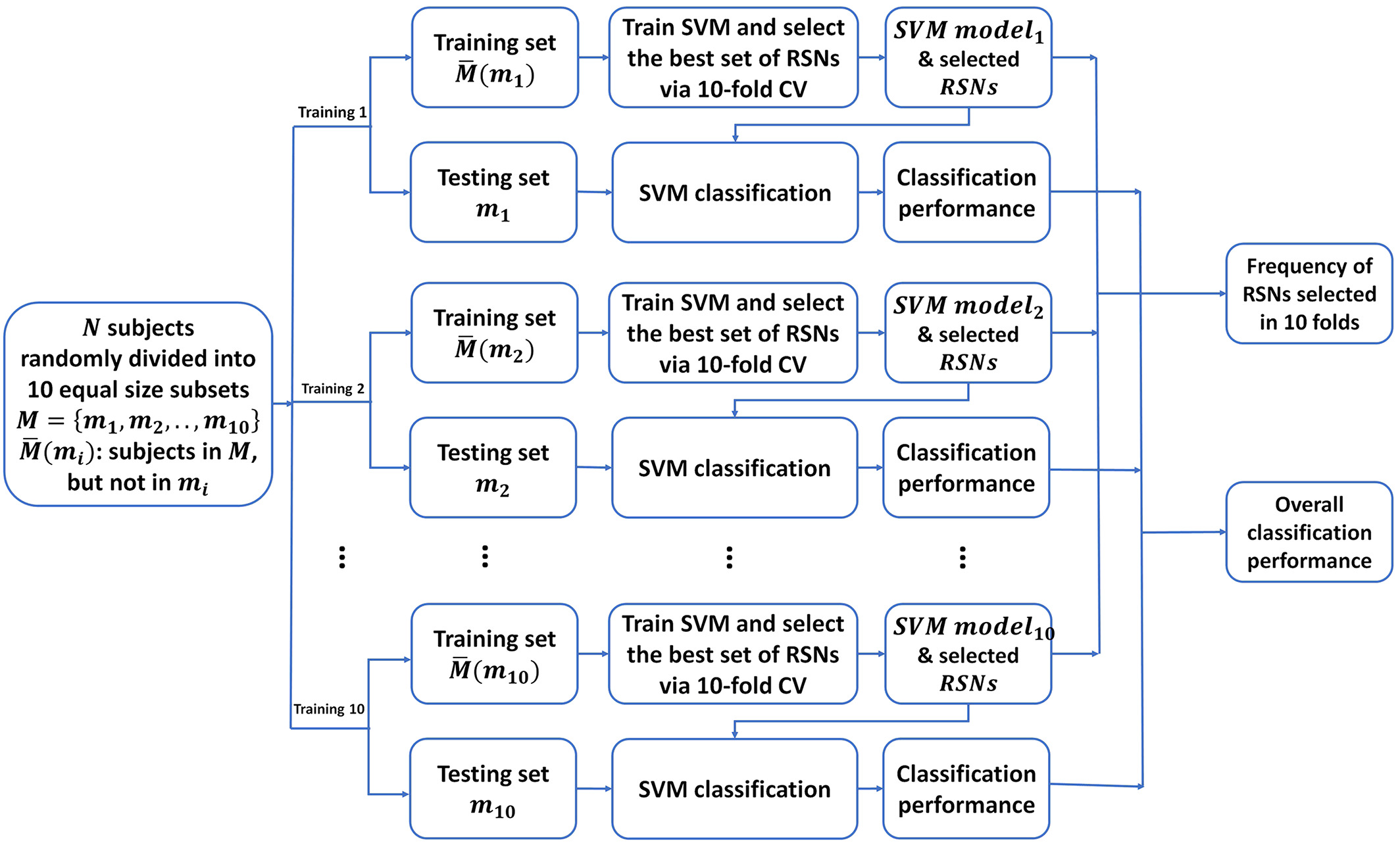
Flowchart of the nested 10‐fold cross‐validation (CV). The dataset is randomly partitioned into 10 subsets, and each of them has the same proportions of individuals with nicotine use disorder and controls. Of the 10 subsets, nine subsets are used as training data to build a classification model, and the remaining subset is retained as the test data for testing the classification model and estimating the classification performance. The CV process is then repeated 10 times (the folds), with each of the 10 subsets used exactly once as the test data. The 10 results from the folds are then pooled to estimate the classification performance. To build the classification model for each fold, a 10‐fold CV is used to select the best set of resting‐state networks (RSNs) and optimize support vector machine (SVM) parameters
cnCV
consensus nested Cross Validation, Bioinformatics, Volume 36, Issue 10, 15 May 2020, Pages 3093–3098
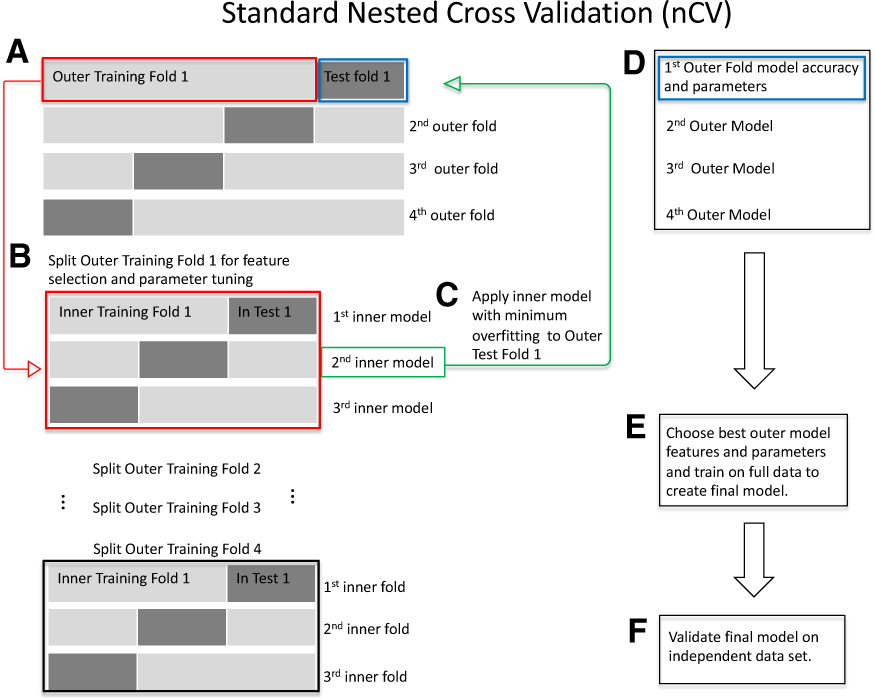
Standard nCV. (A) Split the data into outer folds of training and testing data pairs (four outer folds in this illustration). Then do the following for each outer training fold {illustration starting with Outer Training Fold 1 [red box (A)]}. (B) Split outer training fold into inner folds for feature selection and possible hyperparameter tuning by grid search. (C) Use the best inner training model including features and parameters (second inner model, green box, for illustration) based on minimum overfitting (difference between training and test accuracies) in the inner folds to test on the outer test fold (green arrow to blue box, Test Fold 1). (D) Save the best model for this outer fold including the features and test accuracies. Repeat (B)–(D) for the remaining outer folds. (E) Choose the best outer model with its features based on minimum overfitting. Train on the full data to create the final model. (F) Validate the final model on independent data. (Color version of this figure is available at Bioinformatics online.
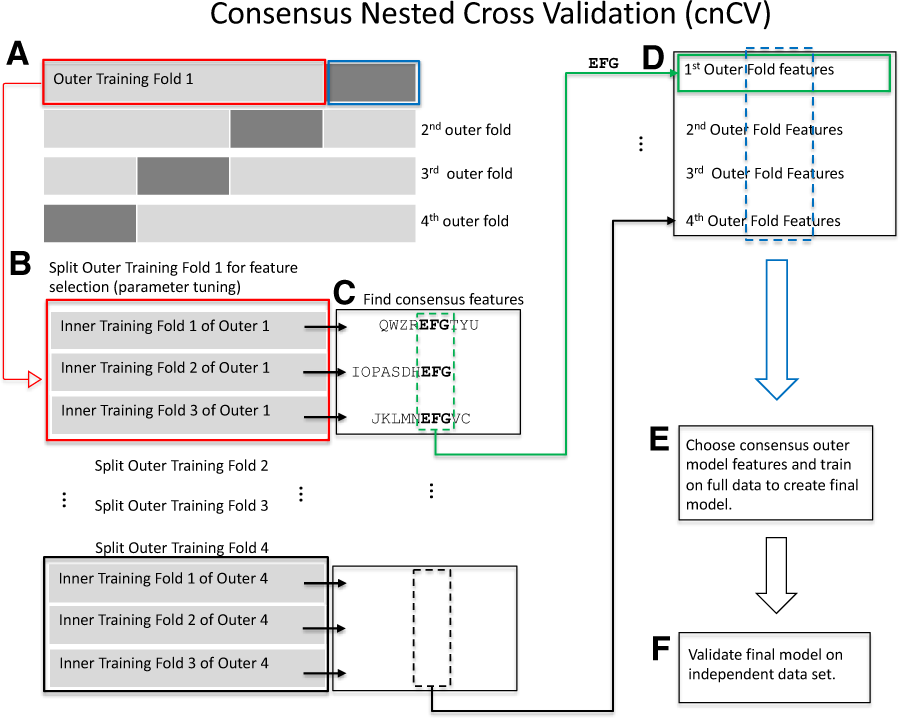
cnCV. (A) Split the data into outer folds (four outer folds in this illustration). Then, do the following for each outer training fold {illustration starting with Outer Training Fold 1 [red box (A)]}. (B) Split outer training fold into inner folds for feature selection and optional hyperparameter tuning by grid search. (C) Find consensus features. For each fold, features with positive Relief scores are collected (e.g. ‘QWZREFGTYU’ for fold 1). Negative Relief scores have high probability of being irrelevant to classification. The implementation allows for different feature importance methods and tuning the number of input features. Consensus features (found in all folds) are used as the best features in the corresponding outer fold. For example, features ‘EFG’ are shared across the three inner folds. This procedure is used in the inner and outer folds of cnCV. Classification is not needed to select consensus features. (D) The best outer-fold features (green arrow to green box) are found for each fold [i.e. repeat (B)–(D) for all outer folds]. (E) Choose the consensus features across all the outer folds to train the final model on full data. Consensus features are selected based on training data only. Classification is not performed until the outer consensus features are selected (A)–(D). (F) Validate the final model on independent data. (Color version of this figure is available at Bioinformatics online.)
scikit
On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation
This example compares non-nested and nested cross-validation strategies on a classifier of the iris data set. Nested cross-validation (CV) is often used to train a model in which hyperparameters also need to be optimized. Nested CV estimates the generalization error of the underlying model and its (hyper)parameter search. Choosing the parameters that maximize non-nested CV biases the model to the dataset, yielding an overly-optimistic score.
Model selection without nested CV uses the same data to tune model parameters and evaluate model performance. Information may thus “leak” into the model and overfit the data. The magnitude of this effect is primarily dependent on the size of the dataset and the stability of the model. See Cawley and Talbot 1 for an analysis of these issues.
To avoid this problem, nested CV effectively uses a series of train/validation/test set splits. In the inner loop (here executed by GridSearchCV), the score is approximately maximized by fitting a model to each training set, and then directly maximized in selecting (hyper)parameters over the validation set. In the outer loop (here in cross_val_score), generalization error is estimated by averaging test set scores over several dataset splits.
The example below uses a support vector classifier with a non-linear kernel to build a model with optimized hyperparameters by grid search. We compare the performance of non-nested and nested CV strategies by taking the difference between their scores.