Count primes

Last updated on Jul 4, 2020 Leetcode

Question

Count the number of prime numbers less than a non-negative number, n.

Example:

Input: 10
Output: 4
Explanation: There are 4 prime numbers less than 10, 
             they are 2, 3, 5, 7.

Solution

option 1 (Define isPrime)


def isPrime(n):
  sqrt = n ** 0.5
  i = 2
  while i <= sqrt:
    if(n % i == 0):
      return False
    i += 1
  return True


def countPrimes(n):
  count = 0
  for i in range(2,n):
    if (isPrime(i)):
      count += 1
  return count
  
countPrimes(9)

## 4

option 2 (Sieve of Eratosthenes algorithm)

def countPrimes2(n):
  
  isPrime = [False,False] + [True] * (n-2)
  i = 2
  
  while i * i < n: 
  # Loop's ending condition is i * i < n instead of i < sqrt(n) 
  # to avoid repeatedly calling an expensive function sqrt().
    if isPrime[i]: # if not prime, it is some prime multiple.
      j = i * i 
      # ex: we can mark off multiples of 5 starting at 5 × 5 = 25, 
      # because 5 × 2 = 10 was already marked off by multiple of 2, 
      # similarly 5 × 3 = 15 was already marked off by multiple of 3. 
      # Therefore, if the current number is p, 
      # we can always mark off multiples of p starting at p2, 
      # then in increments of p: p2 + p, p2 + 2p, ...
      while j < n:
        isPrime[j] = False
        j += 1
    i += 1
  return sum(isPrime)
      
countPrimes2(9)

Summary

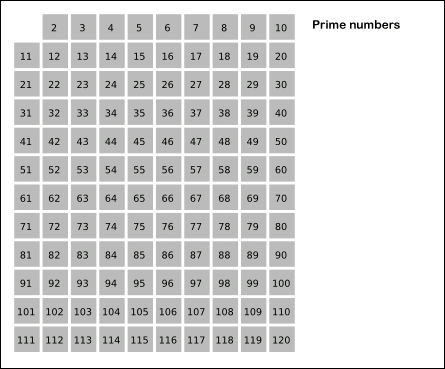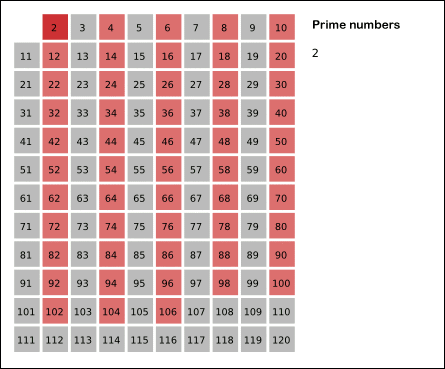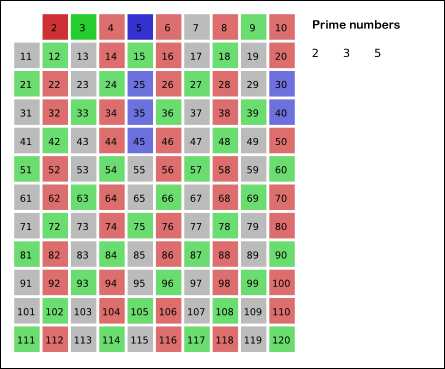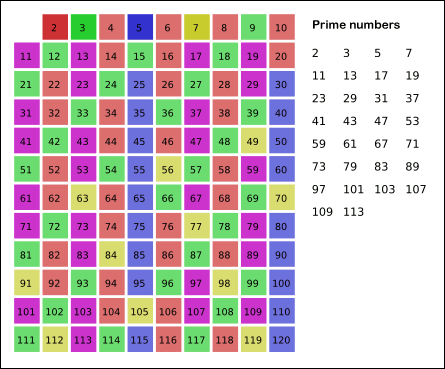
Sieve of Eratosthenes

In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit.

It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with constant difference between them that is equal to that prime.[1] This is the sieve’s key distinction from using trial division to sequentially test each candidate number for divisibility by each prime.

Source: Wiki

Leetcode